About nine months ago I left the sad saga of Jahi McMath behind and moved on, thinking everyone else (including her family) would do the same. Boy, was I ever wrong.
Now this is not the first time I've ever been wrong about something (just ask Mrs. Bastard), but unlike many people, I have no problem admitting when I'm wrong when I've been proven so. I see no purpose in continuing to argue even in the face of overwhelming evidence against me.
But just when I had thought I had heard the end of the story, Jahi's family (along with their lawyer Chris Dolan) came roaring back into the news this week with some rather astonishing claims, and an even more unbelievable request: based on some purported new tests, they are petitioning the court to overturn her death and declare her alive.
I'll give you all a moment to bask in the glow of that mind numbing stupidity before I move on.
One of the main reasons for this request is the contention that Jahi is responding to and following commands. Two videos were released that appear to show just that:
Before anyone rushes to judgment ("It's a hoax! It's a fake! There are strings attached!"), I am reserving judgment on these videos myself. It is possible that she was moving her hand and foot before the camera started rolling (which, by the way, is an obsolete phrase. Cameras don't roll anymore. Non sequitur over.), and that Jahi's family took advantage of her pre-existing spinal reflex movements and recorded them. And before anyone asks, studies show that these type of movements in brain dead patients are not that unusual, occuring in about 1 in 7 brain dead patients. From the article:
The other reflex movements observed in our brain-dead patients were finger and toe jerks, extension at arms and shoulders, and flexion of arms and feet.In case you didn't (or couldn't) watch the videos, these are exactly the movements that Jahi is making.
If that weren't enough, there are other claims made by the family and their lawyer. Apparently she has started menstruating, and Dr. Alan Shewmon, a well-renowned and rather famously anti-brain-death neurologist, claims this proves that she is not brain dead, since the pituitary gland is responsible for secreting the hormones that are responsible for menses. Game, set, and match. Right?
Ah ah ah, not so fast. Studies on brain dead women have revealed that function in both the hypothalamus and the anterior pituitary gland (the portion that produces FSH and LH), is preserved even in brain death. So the fact that Jahi now has her period is interesting, but meaningless.
The family's next assertion to support the "Jahi is alive" line is that an MRI shows preserved brain tissue. Here is a screenshot of her MRI:
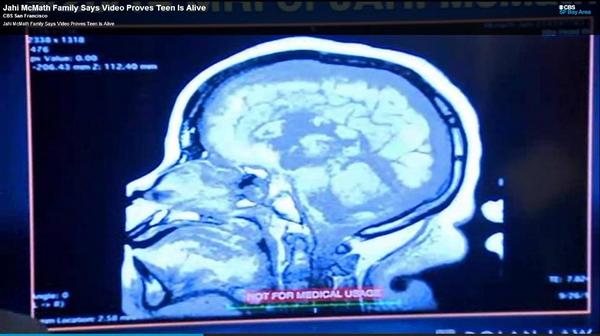
If there are any radiologists looking at this, a comment would be gratefully appreciated. What this shows is catastrophic damage to her midbrain and brain stem, but it does show some preserved cerebral cortex (brain tissue). What this means functionally is impossible to assess based on this one image. This alone doesn't mean she is alive. All I can really say is that there is some brain tissue there. Again, interesting but meaningless.
Perhaps the most astonishing claim is that she has electrical activity in her brain based on a recent EEG. I haven't seen her EEG, but this is enough to make me stop and think. Brain death means a silent brain, so there should be no electrical activity in there at all. If she does have electrical activity, that raises a lot of question marks.
The most telling part of this news is that the doctors supporting these claims hail from the International Brain Research Foundation which is based in the United States. I sure was impressed that such an impressive-sounding foundation would support the idea that Jahi could come back from brain death . . . until I looked into the IBRF and discovered that they are a collection of alternative therapy-driven self-described "mavericks" of brain injury research. To give you an idea of who these people are, their chief medical officer Dr. Jonathan Fellus lost his medical licence this year for having sexual relations with one of his brain-injured patients. It's unethical enough having an extra-marital affair with a patient, but doing it with a brain-injured patient is simply unconscionable (pun intended). If you really want to be creeped out, read the full article.
Not all the doctors who are looking at Jahi are like ex-Dr. Fellus, however. Dr. Calixto Machado, a well-respected Cuban neurologist and author of numerous articles on brain death (including one I have referenced myself), has been asked to evaluate her. Dr. Charles Prestigiacomo, chair of neurosurgery at Rutgers University, has also raised questions based on the results of the various studies (though I'm not sure if either Dr. Machado or Dr. Prestigiacomo has actually examined her).
Damn, this ended up much longer than I was expecting.
Anyway, the bottom line here is that no objective evidence that Jahi McMath is alive has been presented. There must be independent confirmation of the family's claims by a competent doctor. If the claims are verified, then one of the following two statements must be true:
- All six doctors who examined her back in December and declared her brain dead were wrong, they all interpreted her brain death studies incorrectly, and all of the studies showing she was brain dead were wrong, or
- Brain death is not absolute and it is possible to recover, even somewhat.
If the claims are verified, then she is most certainly not dead, and every medical textbook publisher on the planet will have to revise every medical textbook on the subject of brain death. If that time comes, I will readily and freely admit that I was wrong, and every other doctor that believes that brain death equals death and is finite and irreversible will have to do the same.
But if the claims are untrue and/or this turns out to be nothing more than a cruel hoax, then shame on the family, shame on the lawyer, shame on the IBRF, and shame on the media for drawing out this incredibly tragic affair even longer.

This is about money.
ReplyDeleteMamaNails was interviewed by (I think) Essence magazine back in June. At that time she stated that a deceased Jahi could not receive MediCal (California's "insurance" for medically-indegent people), or MediCare or Social Security disability. There's also the little thing about the hospital being "off" the hook because dead people don't need care.
Never mind that GoFundMe donations had slowed to nonexistent. Someone's gotta pay for that house/apartment in New Jersey!
I will always defer to an MD's interpretation of MRIs and such, but that cerebral cortex looks a bit shrunken with gyri and sulci not as sharp or defined as in a really alive brain. The mid-brain/brain stem is alarming, even to my little former RN pea brain.
The person who interpreted the EEG was not a neurologist, nor a person who specializes in brain injury. The "experts" were al carefully cherry-picked and some are rejects from mainstream medicine for a good reason.
I was so hoping you'd weigh in on this!
Of course it's about money.
DeleteThe question is about what they need the money *for*. Right now Jahi is in a Catholic hospital and I'm assuming being funded by Catholic charity. Hospital stays are expensive and she is unable to get insurance. If they're doing this it might be because their benefactor is giving them a dead line on their money.
I'm slightly more sympathetic to a family faking results to keep their daughter "alive". Though in actuality they're most likely seeing typical body reflexes, and with their limited understanding *coughdenialcough* they probably do think she's alive.
Even if the family does get benefits, please keep in mind they are a small amount of money, and it can take years to get. Even if they went the home care route, most of that money would be spent on medical equipment (which is really expensive). They wouldn't have much left over for things other than bills and food.
If the family is honestly after the money because they think they'll be in luxury and getting a free ride, they'll be sorely mistaken to learn that benefits only give enough to take the edge off and afford essentials.
The lawyer on the other hand, is siphoning money for his own selfish purposes. It's in his best interests to keep this circus going. Lawyers are paid to go to court, write legal notices, and "give advice". Once Jahi's plug is pulled, he's out of a job (providing he can't convince them to try and sue).
I'm not a neurologist or in any medical field so any medical image is going to mean little more to me than "Ooh, that looks interesting".
Jahi's corpse is no longer in that hospital. It was...released...shortly after Dr. Fellus had his license revoked, and he was the only doctor on the team with privileges at the hospital. The corpse really is in a home-care setting, with a 24/7 in-home nursing staff paid for by the likes of organizations such as IBRF, TSLHN, Dolan, etc.
DeleteThis has all been more or less confirmed by 3rd party medical professionals with 1st hand knowledge.
I don't doubt you, but how are they doing all these tests in a care home? Wouldn't they have to be at a hospital to access all the equipment necessary to perform those tests?
DeleteIf this is the long awaited neurological miracle for this misguided family, why is their lawyer presenting this to the world via the press and youtube? Would not a team of unbiased neurologists be more appropriate?
ReplyDeleteAlso, question for you doc, if you do not mind? It has been reported that part of this 'experimental' treatment consists of hormone therapy. I can get the link if you like, but would that not also contribute to menarche?
I will await independent verification from outside sources on any claims made by either the family or their shyster, er, uh, lawyer. a youtube video that can be edited to show anything is meaningless to me.
Lastly, I am a new reader, but have covered a lot of ground here on your blog, as your diagnostics will indicate :) I am liking what I read and very much appreciate your efforts in both the surgical theater and here.
The answer to your question about hormones is a solid "Maybe". We have no idea what experimental hocus pocus voodoo magic they're giving her. It's possible.
DeleteHave you read the Neurology extract about what this "dream team" of doctors has done in the past with BD PT's? I think you'll find it very telling in regards to what exactly has been going on here with Jahi's body.
DeleteTake careful note of when it was published, and the people's names attached to the..."work".
http://www.neurology.org/content/82/10_Supplement/P4.285.long
What is your perspective on who administered the MRI, could the MRI been manipulatedprior to release, and are the qualifications of the MRI administrator relevant? Is it typical for MRI's to have Not For Medical Use stamped on them for the simple fact she wasn't a patient at Rutgers? As far as Jahi getting her period, could that have been at least in part to hormones she may or may have received? For 9 months nobody knows what "treatment" she been receiving.
ReplyDeleteThe MRI can't be faked, and I refuse to believe that they're so mendacious that they would substitute someone else's scan for hers.
DeleteThe "Not For Medical Use" is stamped on every copy of every radiologic study to indicate that it is not an original. It means nothing here.
I realize you are a trauma surgeon, and as such your experience is extensive, but I'll state here that I have CD's for every single MRI, CT, etc I've ever had, and I don't see any sort of message anywhere on any of my images. The software comes with the CD they burn for me, and is very professional.
DeleteI may be a little biased here, but I do think it means "at least something", in that they cut some serious corners where they needed to avoid even the smallest questions of credibility, and this is possibly one of them.
You misunderstand me. I'm not referring to those copies which are made for official medical use like you are describing. When copies are made NOT for official medical use (like for presentations), that is printed on them.
DeleteBut aren't they using them for official medical use?
Deletemaking false claims to push a political or economic agenda is not medical use.
DeleteThink of it more like a water mark. The copies that the news is getting is likely a lower resolution version that shouldn't be used for any sort of diagnosis, even from another doctor. I'm pretty sure that a diagnosis like that requires you to look at multiple scans, and you can't make a judgement off only part of the picture. The original medical copies are likely at the hospital. But it can be used to illustrate a point (literally).
DeleteDocB': Thank you for your clarification of what you intended to suggest.
Deleteanyone who has lived in a conjunction with a teenage girl knows that menstruation does not automatically demonstrate brain function.
ReplyDeletejokes aside, thank you for the professional opinion and explanation.
but just to be clear - you mentioned "catastrophic damage to the midbrain and brain stem" that's bad, isn't it? I know when I use the term "catastrophic" it is usually bad.
OMG, need the windex!
Deletethank you. which one?
DeleteOne thing that occurred to me is the issue of patient abandonment. If Jahi McMath had any hope of recovery, wouldn't the hospital in NJ be prohibited from agreeing to her transfer to an apartment? My limited understand of medical abandonment is that doctors (and hospitals) aren't able to terminate a caregiver relationship without transferring care to another provider where a critical need for treatment is involved - like a vent.
ReplyDeleteThis was an issue with Children's Hospital prior to the court determination that the McMath family could transfer her body from the hospital without a designated receiving facility, and I can't imagine that issue simply disappeared with a change in states. If there were, in fact, any realistic hope of recovery, that child would still be in ICU.
-VenomousFeminist
DocBastard: You are not a neurologist and I've come to the conclusion that you need to brush up on neurology.
ReplyDeleteOh boy, a troll. Haven't had one of them for a while.
DeleteBut ok, I'll bite. You're right, I'm not a neurologist. So please do tell me where I went wrong. I'm always ready for some education.
Just an FYI, GoldenShellback1 is a fail troll(John Benton, Johnny Bandana) who has been on the Jahi boards from the beginning. He has claimed at various times to be a marine, CCT RT, criminalist, Physician Asst, medical malpractice investigator and other professions as he feels the need to create them. When he get's mad he makes death threats( has done that multiple times to me personally). He has posted dead baby pics on FB when he was mad. I can provide proof if you want.
Deletecool, so he can beat the shit out of someone, promptly investigate 'who dunnit' and then mend his victim right up. whatta guy!
DeleteIt's very simple. I can post UDDA's guidelines if you like. I'll post them anyway.
Delete"An individual who has sustained either (1) irreversible cessation of circulatory and respiratory functions, or (2) irreversible cessation of all functions of the entire ENTIRE BRAIN, including the brain stem, is dead."
According to ahi's MRI/MRA scan her brainstem was severely damaged . However, the MRA also demonstrated sufficient intracranial blood flow which kept the cerebrum and the cerebral cortex alive for 9 months. If the cerebrum is functioning then Jahi's death certificate needs to be reversed, because the MRI/MRA showed her brain was not entirely dead. If that is the case then the brain death criteria can no longer be applied.
And yet, we have not been presented with any concrete, irrefutable, unbiased evidence that even suggests such a mistake was made. All we've been presented with is Skype-from-Cuba testimonials and unlicensed, unqualified, agenda zealots who've rejected the concept of brain death their entire careers, let alone upon presentation of the McMath case. In other words, Dolan cherry picked a group of profiteering diploma-mill miscreants who would be willing to state - from a non-extradition territory - that they brought a corpse back to life...forgetting that we already have Neurology publications stating these same men have been artificially experimenting on BD cases with Frankenstein-ish procedures for years, and the McMath case was just another opportunity to perpetuate their own agendas.
DeleteIn other words, troll, Dolan is full of shit, the family is full of shit, and there's not a person on this earth with a legitimate medical license willing to risk everything just to help this 3-ring circus continue.
Or do we even need to address the fact that the first "world-renowned doctor" Dolan quoted as treating Jahi in New Jersey had his license revoked for partaking in sexual relationships with his brain-damaged patients? And shortly after that happened, Jahi "was able to leave the hospital in New Jersey to go to home care".
DeleteFace it. There's not a single reputable shred of evidence yet presented, or person risking their neck, that offers any credibility to the family's claim. What we do have, however, is plenty of damning testimonials and evidence from their own mouths (particularly the mother) stating that this as only about money, and they would get rid of their own children if they became a problem to them.
and this matters to the troll, how?
DeleteJohnny, give it up. They know who you are and that you are full of it. Even if you were a PA DocBastard is light years ahead of you. Of course from your previous posts on other boards Your supposed medical experience has been discredited by real medical professionals. Please continue though. This should be hilarious.
DeleteI'm sure it will continue as long as it continues getting attention...
DeleteI'm hoping DocBastard can block/ban him. He tried the same thing on sprockets and I let them knew who he was there too.
DeleteYou know nothing, John Benton.
DeleteOh hell no! Johnny is here too? How many websites has he trolled? 5,000,000?
Deleteanything that pops up on a google search for McMath. he's not a troll, he's a stalker.
DeleteThe MRI and MRA do not lie. It's a concrete piece of evidence. If it can detect intracranial blood flow which is keeping the cerebrum alive, we can conclude that her brain is not entirely dead. She no longer meets the criteria.
ReplyDeletebut you lie. and until it can be proven by UNBIASED DOCTORS - which, I might remind, YOU are NOT. the MRI only shows that brain tissue is not ALL rotting, the alleged EEG is presented by a very unreliable source, AND if EEG is anything like heart monitors, it is pretty easy to present a false trace on one; and you are the only one who has mentioned an MRA at all.
Deletehowever, an MRA only shows that blood is flowing. flowing blood does not mean life, even by the definitions YOU supplied.
however, if they remove the ventilator, and she stops breathing, that is pretty definite evidence that she is dead.
GoldenShellback - I've heard nothing about an MRA. If you have evidence of that, please share it with the group or STFU.
DeleteIt is true that adult elephants can’t jump. But there are other mammals that can’t either, like sloths, hippos and rhinos. Although, unlike elephants, hippos and rhinos can have all four feet off the ground at the same time when they run.
Delete"however, if they remove the ventilator, and she stops breathing, that is pretty definite evidence that she is dead."
DeleteBit of a sloppy definition. There's plenty of people on ventilators that are perfectly alert and alive. Their lungs just aren't working the way they should.
I agree with you though. But the problem will solve itself when the court gets their own specialists to go in and look at Jahi and make sure that all medical information presented is accurate.
I've had several EEGs in my life because of Epilepsy. A psychologist "reading" the EEG should/would be discredited in court. First, you do have to have a trained tech to run the test, especially since each little sensor has to be placed on the correct place. It lasts generally 45minutes and to stimulate brain activity a strobe light is used. Unlike a heart monitor there is no way to manipulate for any sort of false reading. There is the baseline reading and activity measured using the strobe. Only a neurologist would know how to properly read an EEG. I've read several times a EEG was performed because she "responded" to her mom's voice. Dolan and the family are really playing to the "sheeple" who have no idea how any of these test are performed and who actually reads/interpret the results. I seriously can not wait for the courts to say, "yes we are going to appoint our own specialist to perform these same test."
DeleteSadly, this is all a publicity stunt to get Dolan's Prop. 46 passed here in California in November. You watch, he will put off allowing any independent exams to be done on Jahi until after the vote. It's tragic that this little girl is being used as a pawn for so many people. :( The vote in our house on Prop. 46 will be NO.
ReplyDeletewhy... am I not surprised?
DeleteI see why Dolan wants it to pass:
Delete"If approved by voters, the initiative will:[1]
Increase the state's cap on non-economic damages that can be assessed in medical negligence lawsuits to over $1 million from the current cap of $250,000. "
And....Dolan cancels the court hearing for Thursday and asks for it to be rescheduled to November 6th. Two days after the California elections. Why? He doesn't want the court appointed consultant/expert Dr. Paul Fischer to review the data or test Jahi. Sure wish I could predict lotto numbers as well as behavior from this lawyer.
DeleteMost troubling to me is the celebration of her caregivers that she twitches her foot, flicks her hand and menstruates....if this is all that they require to continue to keep her trapped in a bed on a vent indefinitely then there are a few more neuro exams that need to be done. I have seen similar attempts to relentlessly flog some poor child in a similarly futile state many times. It should be a crime.
ReplyDeleteI agree. I have worked critical care for 11 years. Just put in an application for another field of nursing because I am fining it harder and harder to care for the bodies in the bed just to make the family happy. Please God, never let that happen to me.
DeleteRight there with you. I said uncle.
DeleteLet's assume for a moment that she has actually come back to life. The real question is, even if she isn't fully brain dead, is this really a quality of life worth forcing her to endure? Being trapped in a coma/vegetative state the rest of her life seems cruel.
ReplyDeleteIt's not just about Jahi. It's also about an obsolete brain death criteria invented by Harvard in 1968. The same obsolete brain death criteria that is being shoved down people's throat especially the ones who can't think for themselves. The sheeples. The followers. The non-critical thinkers. The YES, I will agree with whatever doctors tell me especially when there are six of them mentality. It's sad but these people need to wake up. This fight is not about doctors or hospitals. It's about insurance companies. The notion of “brain death” was formulated and published by an ad hoc committee of the Harvard Medical School in 1968 which was funded by insurance companies to promote their own agenda. So there you go.
DeleteYou're cherry picking. You're trying to make it sound like 3 different certified neurologists in December, 2013, used medical technology and standards from 1968 to form a diagnosis by today's standards.
DeleteThis is not only hurting your argument, but is really absurd.
Cherry picking? I don't think so. The UDDA is based on the Harvard Ad Hoc Committee's report. You might want to think why insurance companies funded Harvard to invent a guideline on brain death.
DeleteWhat's the matter Johnny boy? Can't give DocBastard the proof he's asking for? Color me surprised.
DeleteGoldenShellback - No, brain death was NOT "invented" at or by Harvard in 1968, a fabrication I see thrown around every time the subject of brain death comes up. The concept of brain death first arose in the late 19th century, and it evolved over time. The ad hoc committee report you mentioned only summarised what was already known and tried to establish a unifying paradigm for establishing death by neurologic criteria.
DeleteAnd before you try the next argument that brain death opponents make, that brain death was created so that ghoulish transplant surgeons could harvest organs, that's not true either. Transplantation and brain death evolved separately.
Here is the truth of the matter: http://www.ncbi.nlm.nih.gov/pmc/articles/PMC2652772/
This comment has been removed by the author.
DeleteMairzy doats and dozy doats
DeleteAnd liddle lamzy divey
A kiddley divey too,
Wouldn't you?
My question is,...with the amount of brain atrophy/damage is it even possible for her to hear the "commands" her mother gives her. I ask this in jest, as I do not believe it is possible for her to "do" anything.
ReplyDeleteWithout seeing every mm slice of the CT (or perhaps more reliably, an MRI) it's really impossible, I would think, to know for certain if there's even any nerve tissue connecting the auditory "organs" to the remaining brain mass.
DeleteAs was already suggested (either here or elsewhere), we've seen a single, central CT slice of the brain, which was likely the BEST one they could find in all the images (very telling, since it shows serious structural problems). This is for good reason.
So Machado's declaration to the court says she is not brain dead because "ribbons of neocortex" are present on the MRI which indicates blood flow to the brain. He says he expects her brain would be completely liquified by now. He does not mention an MRA was done. What he says indicates he was not present when the EEG was performed in the apartment she's at.
ReplyDeleteHe's very careful in his wording and even though he mentions the AAN criteria he does not indicate he performed any of the tests that follow those criteria.
links to the declarations filed: http://www.thaddeuspope.Com/futilitycases.html
Deletein the complete declaration in the link provided he does mention the MRA. "slow but intracranial cerebral blood flow".
DeleteIt appears there is a picture of the MRA on the last page of Dolan's declaration.
DeleteSo, am I correct to understand that anyone's goal - the lawyer's, the family's...is to have untold millions of CA taxpayer dollars pay for a girl who will never walk, talk, communicate, movepurposefully - while thousands die in W. Africa for want of care that could be provided with a fraction of that amount of money?
ReplyDeleteI never speak for Jesus the way some on Twitter do.
I'll make this exception: Jesus would weep. Think of all those that could be saved, for want of rehydration, IV's, even *bleach*... And this poor girl in a bed, not here, not there, her family a circus.
It is shameful and I truly hope that credible doctors, journalists, lawyers...take this on.
I agree with part of what you say, what pisses me off is don't ask me to take care of someone else's children and not my own. There are children who go to bed every night hungry in this country. Only meals they get is what they can get at school. And what scares me most is what of the children who are not school age yet, what about the single parents who go to bed without food, because they can't afford gas, gro, rent, bills, etc "and what little food they do have goes to their little ones" because they have to try to survive on minimum wage here in the states. I would never ask you to put my children in front of your children. So please don't ask me to put the children of another country in front of the children of mine. Take care of your own first, then what's left take care of others. To others I apologize for being off topic, but please take care of your own first.
DeleteWe're already paying millions of dollars for brain dead politicians to sit around doing nothing. :D (Seriously... $174,000 a year per congressman...).
DeleteTo Candy's point though, parents aren't left high and dry. I got pregnant while I was dead broke and there a lot of resources out there for mothers and children. There's WIC for under 5's, then at school they get free lunch. There's also SNAP (food stamps), TANF (welfare), C-CAP (Childcare), Utility Adjustments, Subsidized housing, Medicaid, Free weather proofing to save on heating, free cell phones.
On top of that, all you have to do is walk into a food bank and tell them you're hungry. Most will be willing to give you food without question, some will ask you to volunteer there to help out and give back.
Which is why I get pissed off at corporations paying minimum wage. We're paying to support their workers that they could easily, *easily*, pay enough to make it above the poverty line and afford all that, and the most pay raise we'd see is a few cents on products. Instead they're choosing to cut corners and making taxpayers pay their workers.
it is not the brain dead politicians I resent so much as the money grubbing CEOs who make up to a hundred times what a congressman makes (or more) - and demands that he must be able to pay lower taxes, or he will lay off employees.
Deleteand yes, when you buy that cheaper (in every way) product at walmart, you are voting to raise your own taxes to cover increased public assistance costs. - the walton kids, who are 4 of the ten richest people in America, are padding their own paychecks with your welfare dollars.
That's now how taxes work. Boycotting Walmart hurts Walmart about as much as boycotting meat hurts the slaughterhouses. Don't be naive.
DeleteWalmart or any other corporation will not lay off employees for the same reason they won't hire new ones: They only hire the required amount to keep the place running smoothly.
The top 1% of the country already pay almost all the taxes considering lower income brackets get bigger returns. The US is the last refuge for corporations as far as tax breaks go. They can whine all they want about tax increases, they have no where else to go.
The only way you're allowing your tax dollars to go towards stupid shit is by not getting out there and voting.
not quite true. by not buying cheaply made stuff at WalMart, I am getting better quality stuff at local sellers, which helps the owners and employees of the locally owned store. if enough people shop at the locally owned store, they will need to hire more personnel to keep up with demand, and they will be happy to pick up employees from walmart.
Deletethe common term for this is investing in your community. by buying from a local person I put money into his pocket, and then later, that money will eventually circulate around to someone who wants to buy my services from me.
but you're correct that we don't have to kowtow to the corporations. I'm not advocating boycotting walmart and thinking that they will notice losing one customer. I am advocating understanding the hidden costs of what appears to be a good deal.
as far as the 1% paying most of the taxes - that is true in an absolute sense, but false in a relative sense. yes they pay most of the tax dollars, but they also get most of the income dollars, and a higher percentage of the profit dollars than the percentage of tax dollars they pay. the relevant point is that by allowing them to control the market, we have allowed them to socialize their expenses and privatize their profits.
DeleteCandy I think you miss the point of the whole discussion which is the atrocity of this child being kept animated by machines when she has long since passed. Instead you go all Ayn Rand and drag politics and selfish behavior into it. I agree most emphatically that this family should get nothing for their fraud, but stop with the whole don't put other kids before my own. I'm a parent and let me tell you if one of them came home with a classmate who was in need of a hot meal or decent clothing, I'd give what I could without question. I highly doubt any court is going to overturn a declaration of death much less award welfare or disability payments to a dead person.
DeleteI think you have missed Candy's point, which is not that if her kids brought a hungry child home that she would not feet the child - her point is that if her children came home hungry, and a collector came to the door collecting for hungry children in Imaginistan, she would feed her own children before making a donation for Imaginistan.
DeleteMr Bas, I have been trying to find out who the 3 additional doctors are that examined Jahi at CHO.Court records state that the family brought in 3 independent physicians and all 3 confirmed the diagnosis of BD. None of these doctors are listed in court records . If these doctors did not work there wouldn't the hospitalhave to give them privileges temporarily to examine her? If 3 additional independent docs evaluated her then why did judge Grillo feel it necessary to bring in Dr Fisher?
ReplyDeleteNotice that the Xray says "Not For Medical Usage"???
ReplyDeleteDocB has already pointed out (yes I know the comments are getting to be a wall of text) that the presence of that stamp only indicates it is a copy made for outside publication, and that the stamp, by itself, does not indicate either validity or invalidity.
DeleteSo what I am seeing on the MRI (and no, I am not a neurologist) is multiple areas of infarcts, calcification, dilated ventricles, atrophy and an almost completely obliterated pons. Microcirculation could exist, but that would be woefully inadequate to maintain brain function.
ReplyDeletehttp://www.nj.com/news/index.ssf/2012/01/meadowlands_hospital_neuroscie.html
ReplyDeleteThe CEO of the IRBF lost his last job because he was performing unapproved treatments on children.
Mr Bas,according to Chris Dolans declaration of Oct 3 Childrens Hospital had taken the position that NO doctors outside of CHO could examine Jahi. after their initial diagnosis of brain death.WHy have I seen in court papers that the family brought in THREE independent doctors?? I fst noticed this back in DEc when Tad pope had presented some of the earlier docs.It was confirmed after accessed Justia.com and reviewed more of the court documents.This just sounds odd to me.I thin k it was Doug Straus making the claim but not sure. What do you think?
ReplyDeletewhat's with the Mr Bas? And what's with repeatedly bringing up old news about who did the examinations last year? How about sticking to the topic?
Deletewell he calls hife wife "Mrs Bas**** and I am reluctant to use derogatory terms even if they are in jest. The old news has me very curious because no one knows who these people are.CHO declined to ket anyone else do an exam yet their attorney claims 3 did.
DeleteSheesh. He's not a "Mr" he's a "Doc Bas***" so if you're reluctant to use derogatory terms than just refer to him as "Dr Bas" or just "Doc". The old news is irrelevant regardless of your curiosity which is probably why you didn't get an answer the first time you asked. Continuing to repeat the same question is starting to border on spamming, imo.
DeleteI hadn't replied because I didn't realise "Mr Bas" referred to me. I call myself "DocBastard", so if I don't censor myself, don't feel you need to do so yourself. "Doc" is fine, as are DB, DocB, Hey You, etc.
DeleteI don't know who the other doctors are, but it is my understanding that several physicians confirmed her brain death diagnosis before Dr. Fisher did. The only way to confirm their identities would be to access the medical records. The family has made it quite clear that they have no intention of letting that happen.
You are missing the point entirely,sir. CHO declined to let ANY doctors examine Jahi or provide the family with medical records,yet on their court statement of DEc 20 well before Jahi left CHO they claimed the family brought in 3 doctors already.Think about this for a second.CHO would have to have givn temporary privileges would they not? Why would the judge feel it necessary for a forth independent Dr (Fisher) to do another exam?
DeleteLet me refresh your memory if you have not read any of the readily available documents. Dr Shanahan,Dr Heidersbach, and Dr Fisher did BD exams on Jahi.Dr Shanahan did "the Test" as she referred to it on the 11th.The apnea test performed lasted 15 minutes.On the 12th of dec Dr Heidersbach did another confirmatory exam and apnea test. On the 23rd Dr Fisher performed the final exam. The apnea test was concluded after 9 minutes and her PO2 level reaching 73.3 Dr Flori is the Dr who cared for Jahi and whose report appeared online stating that Jahi was decomposing already as evidenced in her statement that she was sloughing her bowel lining and the appearance of her skin. Dr Gospe was a pediatrician who did not see Jahi but whose declaration on spinal reflex movement was used to refute DR Byrnes testimony. Dr Durand was the chief of peds I believe. Dr Ann Petru was a member of the ethics committee. These docs are all identified in court records yet the 3 independent physicians brought in and supposedly approved by the Mcmath family are never mentioned or referred to again
DeleteYou've almost got it... the family proceed several unqualified doctors to do Jahi's examination (a few of whom have shown up in the latest rounds of court documents) and CHO refused to rant them privileges. The court agreed and appointed Dr. Fisher as the independent expert. Since the doctors performing brain death procedures always have a colleague present (to protect them and the patient, they never do this alone - it's very serious work), there are a total of 6 qualified doctors who agree with the finding of brain death.
ReplyDeleteHere is what Dr Fisher had to say about the new tests.
ReplyDeletehttp://www.miamiherald.com/living/health-fitness/article2624741.html#/tabPane=tabs-2b852ffe-1
Isn't that interesting. He basically said what I did - await independent confirmation and/or new information.
DeleteThe court documents from Dec state that Jahis family had THREE independent physicians examine jahi and declared her brain dead. Mr Bas would not the hospital have to grant them privileges to do a proper exam? No where in the documents are they identified..
DeleteDoc, if you get a chance to read his letter what he basically says is that their tests are bunk. His letter starts on pg. 5: https://www.dropbox.com/s/nacvrwtpa5w6jqv/McMath_Linked_File.pdf?dl=0
DeleteAccepted medical guidelines: movement. preserved hypothalamic function,blood flow to the brain,minmal EEG activity,and preserved pituitary function do not preclude a diagnosis of BD.The important feature is lack of brainstem function as evidenced by lack of 7 reflexes and the inability to breath and of course being in a coma of know origin.
DeleteDoc...why do these people and the attorney, keep referring to brain swelling? What could have caused brain swelling in the beginning of this saga?
ReplyDeleteI believe the swelling they are referring to may have been the result of a reperfusion injury following her code. Though to be so severe that it would result in an absence of blood flow several days later would seem to be unlikely.
DeleteAccording to documents her brain was about 2/3 swollen post arrest. I am not sure if this assessment was based on a CT scan Her stepfather in an interview claimed the family was told around the 10th that Jahis brain was half dead and then a day later she was 100% brain dead. He does not say which medical personnel revealed the info,but I assume it was one of the doctors caring for Jahi. There is nothing in any documents of any attempt to address the swelling or when and why she was prescribed the vasopressin she was on as revealed by Dr Fishers report,
DeleteThe brain is either alive or dead, not "half dead", not "mostly dead". Vasopressin would have been administered to maintain perfusion to the heart, kidneys and brain. It's use would have been documented on Jahi's medical records, which were not released because the mother did not consent to their release. As to which date the ct scan showed brain swelling, it would most likely be prior to the first test to determine whether or not she was brain dead. Again, most likely in the first 24-48 hours following her cardiac arrest.
DeleteThe vasopressin IS listed on Jahis medical record related to Fishers exam.I can provide a link if you do not believe me.In the court transcript of DEc 24 the judge allows the results to be released for public scrutiny.The medical record shows she was on vasopressin as well as artificial tears.Yes vasopressin in used to keep organs perfused especially in cases of organ donation.
DeleteHere's what they're not telling you about Fisher and Stanford:
ReplyDeleteStanford did a study saying that T&A is safe. As a result, Stanford promoted the study to pediatricians and ENTs.
Fisher works for Stanford and therefore should not be involved in this case due to conflict of interest.
I have forwarded this to Dolan.
No, "Stanford" did not do any study. Perhaps one of the hundreds of doctors and/or researchers who work at Stanford may have done a study regarding tonsillectomy. But Dr. Fisher is the chief of paediatric neurology, not an ENT or tonsillectomy researcher, nor is he someone who has anything to do with the procedure. So there is no conflict of interest.
DeleteI would say nice try, but it wasn't. But for the benefit of everyone, please let us know the tonsillectomy study to which you are referring. I'm looking forward to reading it and figuring out exactly what this has to do with anything.
You failed in your research. I'll let you try again Fisher will be judicially removed from this hearing.
DeleteFisher may not be directly involved with the study but he still works for Stanford.
DeleteGoldenShellback19 October 2014 23:56
DeleteFisher may not be directly involved with the study but he still works for Stanford.
-----------------
Again, so? The purpose of this hearing is not to determine whether or not T&A's for sleep apnea are safe. The purpose of the hearing is to determine whether or not Jahi's body still meets the criteria for brain death. It should also be pointed out, again, that the T&A was only one of 3 procedures she had performed on her in December.
By your line of reasoning, all of Dolan's so called experts should be excluded because they have publicly stated they don't believe in the existence of brain death. Therefore, their conclusions as to whether or not Jahi's body still fits that criteria is inherently biased.
ga_mom : It's up to the judge to decide. Fisher could be dismissed from this hearing based on conflict of interest. The judge will make that decision, not you.
DeleteNor will you. Your argument to exclude him is inherently flawed, no matter how much you stomp your feet about it.
DeleteIf Fisher disagree with Dolan then Dolan should ask the court to perform 18F-FDG-PET scan on Jahi. This will settle the issue: "18-Fluorodeoxyglucose (FDG) positron emission tomography (PET) with its superior spatial resolution as compared to planar or SPECT imaging and the capability to directly visualize brainstem metabolism have the potential to overcome the problem of adequate visualization of the brainstem. It has been described in the literature, [32] but is not specifically mentioned by any of the professional societies in the USA as a recommended method for the confirmation of brain death."
DeleteYou've been trotting out that same tired line for the last 10 months.
DeleteI think this whole idea of having a judge reverse a death certificate is absurd.The judge did not declare her dead and has no authority in this matter. NO doctor even signed her death certificate which is probably not even a valid document considering she is and has always been very much alive.
DeleteShe's dead as a door nail.
DeleteI don't follow.
DeleteYou... want to pump a girl full of radioactive material for a test that isn't even a recommended method to confirm brain death?
sorry,mom dead people do not make purposeful movements. The mechanism of supposed spinal reflex is unknown yet widely accepted as fact in the medical field.
DeleteI think that may be one of the reasons judge Grillo extended the TRO twice and left it up to the higher court.Distinguishing between the reflexes of a supposed corpse and a disabled human was not his expertise. Even Dr Gospe and the info provided to the court by CHO counsel states that they still do not understand why some BD patients move.
Shark,the only recommended and required test is a clinical bedside exam with proof of apnea.The law states it must be by accepted medical standards .The BD test basically confirms lack of brainstem function and about 7 reflexes and is really not a whole brain test.EEGS CTs MRIs and CBF are not even required.
Delete"sorry,mom dead people do not make purposeful movements."
DeleteYou should visit a morgue sometime. They can moan too.
Yes, that goes back to my original point to Golden Boy wanting to do a PET scan on her.
DeletePET scans use radioactive glucose and are normally for detecting cancer and other abnormalities. I don't think it's going to pick up brain activity any better than an MRI or any other test that's been done on her already.
It was just a tongue in cheek remark.
Shark: You are dead wrong. SPECT scan also uses a radio active material to penetrate the blood brain barrier. The same SPECT scan that was performed on Jahi to support their BD diagnosis. 18F-FDG-PET scan is not just for detecting cancer read below:
Delete[Clinical application of 18F-FDG-PET in patients with brain death].
[Article in Japanese]
Momose T1, Nishikawa J, Watanabe T, Ohtake T, Sasaki Y, Sasaki M, Mii K.
Author information
Abstract
In order to evaluate glucose metabolism in brain death, 18F-FDG-PET scans were performed in three patients with clinically highly suspected brain death. One case was caused by head trauma and other two cases were by subarachnoid hemorrhage. All of them were in deep coma without spontaneous breathing, whose intracranial pressure was remarkably elevated up to the level of mean arterial pressure. Nineteen frames of dynamic scan were started soon after intravenous injection of 18F-FDG for one minute per frame, followed by 10 minutes of static scan which started 40 minutes after the injection. Both in dynamic and static scan, no significant intracranial accumulation of 18F-FDG was seen in all of three cases. This finding can be interpreted as the evidence that there is no significant glucose utilization from blood in the brain. This is the first report of clinical application of 18F-FDG-PET to brain death. Our results support the clinical diagnosis of brain death and 18F-FDG-PET can be of value for the assessment of glucose metabolism in patients with suspected brain death.
Oh. So you want the defining test, the be all end all exam, that will be the defining evidence, to be a PET scan based on a study that used a sample size... of three.
DeleteWell, by all means, let's do it!
Your test still isn't required by law. Go challenge the law first. Good to know you still lack the ability to process information.
DeleteWhy not do it? If the brain can metabolize glucose, it's not dead. It's that simple.
DeleteI was agreeing with you.
DeleteYou should email Dolan. This is serious stuff.
copy/paste, copy/paste. how we love to copy/paste. comprehension doesn't count as long as we can copy/paste.
DeleteShark10 October 2014 04:25
Delete"sorry,mom dead people do not make purposeful movements."
You should visit a morgue sometime. They can moan too.
-----------------------------
That's not the same as a purposeful movement.
Are you saying Jahi has purposeful movement now? A moment ago you were just saying she was dead as a door nail.
DeleteGoldenshellback1- a 18F-FDG-PET scan would not be applicable. The absence or presence of blood flow is not one of the criteria for determining brain death.
DeleteAnonymous: The 18F-FDG-PET detects metabolism or sugar uptake in the brain. Dead brains don't metabolize glucose!
DeleteAgain, Goldenshellback1, blood flow does not equate to a functioning brain. I know this is difficult for you to understand, but even in the absence of oxygen, cells continue to metabolize glucose. It's called anabolic metabolism. There is a reason the PET scan has not been adopted ANYWHERE as a means of determining brain death.
DeleteNow, I totally get that you like the idea of playing Dr Frankenstein with this girl's body. In fact, I think you kind of get off on it, to be perfectly frank. Thankfully, the rest of the cognizant world has more sense.
Baloney. If blood flow does not equate to a functioning brain then why did they perform a SPECT scan on Jahi? Answer that one genius. And if the brain is metabolizing glucose that process is called carbohydrate metabolism not anabolic metabolism. Try again.
Deletejohnny you're still an idiot. The law is the law and Dolan isn't trying to change the law. The court is either just going to say no or order the testing required by law. You FAIL. AGAIN.
Delete"Dolan isn't trying to change the law"?
DeleteThat doesn't even make any sense at all. That sounds like idiotic to me.
You don't recognize your own idiocy so no faith there. The law wins. You lose.
Delete"The law wins"
DeleteBWAHAHAHA!
You claim to have the knowledge yet you can't dispute it. I wonder what that could mean....
DeleteRote memorization =/= understanding.
DeleteI'm breakin' rocks in the hot sun
DeleteI fought the law and the law won
I fought the law and the law won
I needed money 'cause I had none
I fought the law and the law won
I fought the law and the law won
I miss my baby and I feel so sad
I guess my race is run
Like she's the best girl I ever had
I fought the law and the law won
I fought the law and the law won
These are the ESTABLISHED guidelines for determining brain death. Nothing Dolan nor his minions say will change this.
Deletehttp://pntb.org/wordpress/wp-content/uploads/Nakagawa-Crit-Care-Med-2011-Update-Ped-BD-Guidelines.pdf
The "established" guidelines for determining brain death was invented in 1968. They didn't have PET scanners back then so it's obsolete and outdated.
Delete"guidelines" is plural and "It's" is singular.
DeleteGuidelines for determining brain death in children were revised in 2011.
DeleteThis comment has been removed by the author.
ReplyDeleteOnly America.
ReplyDeleteYeah, we all saw what happened when you guys tried doing Black Friday last year. You're no better than us. ;)
DeleteAny physicians or medical personnel care to comment on the administration of vasopressin to Jahi as evidenced by Dr Fishers exam?The results were made public.Dr Shanahan stated in the court records that she prescribed nothing for Jahis Diabetes insipudus wnich she said was evidenced by her extreme urinary output and other tests. Why was vasopressin being used?
ReplyDeleteVasopressin is used to maintain perfusion to the heart, kidneys and brain.
DeleteHow does it perfuse a brain that is 2/3 swollen?
DeleteI thought vasopressin was used as an antidiruretic or to increase blood pressure? Mind you,I am not at all in the medical profession yet am curious as to how the vasopressin is supposed to work to reduce brain swelling.
Deleteit isn't. it is supposed to increase blood pressure to the brain when the heart isn't pumping effectively.
DeleteSo the desire was to increase blood pressure to a swollen brain?
DeleteVasopressin is a vasoconstrictor, and it constricts the splanchnic blood supply (ie blood supply to the gut) to essentially re-route it to the brain. It is supposed to increase the blood flow to the brain in an attempt to keep it perfused with oxygen while the intracranial pressure is high due to brain swelling.
Deleteshort answer: it doesn't reduce the swelling - it just tries to get more blood past the swelling.
DeleteSo how does it work in the managenent of multiorgan donors ? Is it a different dose?Just wondering because that was the only med Jahi was on,and obviously she was prescribed it before they declared her brain dead.
Deleteas I understand it, vasporessin is intended to prevent the person from being eligible to be a posthumous organ donor.
DeleteAnd Golden1 according to accepted medical standards blood flow does NOT preclude the diagnosis of BD,neither does movement.preserved pituitary function,or preserved hypothalamus function,According to the law brain death can be determined by any accepted medical standard.The law is incredibly loose and what it basically does is equate whole brain death with simply brain stem death.Brain stem death is the legal criteria in the UK.If you want to see how the test is conducted there is a brief video on youtube.Also in UK i don't think a second exam is required just that a second doctor verifies the testing by actually observing the first one conducting the exam.
ReplyDeletethe accepted medical standard to determine brain death in a pediatric patient in the US is the one that Dr. Fisher and the other physicians used. Dolan's team didn't use that accepted medical standard and that is what Dr. Fisher said in his letter.
ReplyDeleteYou keep saying blood flow. 18F-FDG-PET for brain death does not measure blood flow. It measures metabolism and glucose uptake in the brain. Don't confuse yourself between SPECT and PET.
Deleteyou keep cutting and pasting stuff out of context. don't confuse yourself between being able to google technobabble and knowing what you are talking about. and besides, canned corn is vastly inferior to frozen corn.
DeleteThis comment has been removed by a blog administrator.
DeleteJohnny, too bad you can't prove it. Also, if you did, no one would care. Besides, why are you here on comment boards instead of using your VAST medical and legal training to get the brain death tests revised to your liking?
DeleteI'm actually working on a petition to revise Harvard's Criteria. I wrote Dr. Shewmon and he seems interested. He wrote me back!
DeleteThat's no better than having Dr Byrne on your side. Have fun with that though. Wish I could be there while they were laughing and burning or shredding your petition. Oh, you're now in contact with Dr Shewmon like you're in contact with Dolan and Jahi's family? Is that like how you sent your research to CHO 8+ months ago that was supposed to make them immediately settle?
DeleteSomeone (who shall remain nameless) just posted a very nasty, offensive comment, which I immediately deleted. Do NOT do that.
ReplyDeleteDoc, personally I think the GoldenShellback 11 October 2014 18:51 post would also qualify.
DeleteWhy? Just because I disagree with your BD criteria, you attack me?
DeleteGoldenShellback - No, because you mention a certain type of videos on a hard drive. This type of comment will not be tolerated, and they will be deleted. Post something like that again, and you're banned. Got it?
DeleteI hope we're clear on this now.
GoldenShellback, just to be clear, there is more than one "Anonymous" posting here.
DeleteDocbastard: Working in the ER doesn't make you a trauma surgeon. You can go ahead and block me now.
DeleteGoldenShellback- No, but being a trauma surgeon makes me a trauma surgeon.
DeleteLet's get one thing straight: this is MY blog, and you are but a guest here. So while you are here, you will abide by my rules. If you break those rules, you will be removed.
I've said it many times before - crying "Fake!" is the final statement of a failure who knows he's lost the argument.
If you have anything constructive to add, then do so. Otherwise, you may feel free to fuck right off.
Johnny you need to learn to play nice. You are a guest here.
DeleteJohnny's lost every argument since he began posting on Jahi threads. He thinks that if he Google's medical stuff it will make him smarter than everyone else. Of course he can't understand the majority of what he reads.
DeleteDocbastard: I understand your dwindling practice/blog but don't get mad at me. Take some anger management courses or something. You might feel better.
DeleteAnd that right there tells you all you need to know about Johnny. It also shows that if he can't Google something he has a hard time thinking on his own. People laugh at what he considers an insult.
DeleteJohn Benton • 22 minutes ago
DeleteDocbastard: I understand your dwindling practice/blog but don't get mad at me. Take some anger management courses or something. You might feel better.
• Reply•Share ›
Hey Doc, John Benton is GoldenShellback1. He posted this on National Review mocking you.
Johnny wants to get banned. He admitted on another board. I'm guess he is claiming to be a master computer hacker and can see things on your hard drive. He's accused several others of the same thing.
ReplyDeleteIt's not that he wants to get banned; it is that he has some form of mental compulsion. he would rather be banned than to be forced to admit that he hasn't got the foggiest idea what he is talking about. that is why it is so easy to derail him by forcing him off script. unfortunately, only he can make the decision to seek the help he needs to break out of this dead end cycle of stalking that he has trapped himself in.
DeleteJohn/GoldenShellback: We all know who you are and your history of posting on this story. There is not a single person who has supported your BS statements on any board, blog, or web page. Your opinions, arguments, and statements have all been ridiculous from day one and have no scientific basis ~ none. Absolutely no one buys your crap.
ReplyDelete"Essentially, what the court does is say, yes, there is a presumption towards preserving life in CA, so let’s get an independent expert in here to resolve the issue of brain death so there’s no question about it on appeal." This is a quote from the blog of a purported lawyer explaining why the TRO was granted. There is a presumption towards preserving life,yet the judge deliberately denied nutrition and antibiotics in his order of Dec 20. It was petitioned for yet crossed off in the doc and basically maintain the status quo to preserve organs. At this point because of what he claimed could be a conflict of interest regarding the fact the two diagnosing physicians worked for the institute where her injury occurred,the judge thought it prudent to bring in an independent expert(DR Fisher).Dr Fisher was recommended by CHO counsel and approved by the family. To his credit though and in a very charitable act,Dr Fisher stated in an email before he examined Jahithat he wanted to donate his fee for the exam ,in Jahi's name ,to 2 childrens charities.His exam was on Dec 23,and according to Chris Dolans recent statement to the press,Dolan was present for the exam. He said that at that time Jahi made absolutely no movements ,concurring with the written words on Dr Fishers exam.
ReplyDeleteThe judge ruled thta the TRO would be dissolved yet gave Nailah time to appeal to a higher court,which she did. An mediation conferemce was ordered by the higher court and on Friday Jan 3 the media reported Jahi was going to be removed from CHO,the coroner issued a death certificate. Jahi was released on Jan 5 to the custody of the Alameda coroner and then he released her to Nailah as a matter of legal protocol. The judge advised Nailah that she was fully responsible for Jahi now,as she may have another cardiac arrest, Upon arrival at the new hospital it was found that Jahi was extremely malnourished as well as having a serious infection. That infection was noted by Dr Flori when she descr9ibed the malodorous discharge in her respiratory secretions. A feeding tube was inserted as well as a trach and 9 months later this sweet little girl is still fighting! If you look at the history of this case,you can see this child survived cardiac arrest, 3 apnea tests,starvation for 28 days,and a severe infection.She is a fighter with the heart of a champion. Praying for her always
she did not survive any of it - her body is being maintained by machines, but it is an empty shell. the brain structure has decayed to the point that there is absolutely no chance of recovery barring the supernatural - and the supernatural's answer gives every indication of being "no."
DeleteIf they had let her go when she died, they would have my sympathy - as it is, they get none from me.
The irony is that you don't understand what a negative apnea test means. She by no means "survived" an apnea test, which is not designed to kill or harm (in fact, if the oxygen level drops at any time during the procedure, the test is aborted). There is no harm in an apnea test. It simply tests the brainstem's ability to detect and respond to an INCREASE IN CARBON DIOXIDE, not a decrease in oxygen. She did not "survive" the apnea test - she failed it.
DeleteStarvation for 28 days? Say what! You seem to forget that what we do know is that Jahi asked for, and was given, at least one popsicle in the immediate post-op period. Supposedly parents of children in the PICU at the same time as ScamFam saw Jahi being fed a cheeseburger, which in all probability is what broke open her raw oropharynx.
DeleteI am guessing that she also received a 5% dextrose solution at some point (I can't remember if this is a known fact based on the few medical records we've seen). Humans can go quite a long time without eating, and poor Jahi had plenty of reserves.
Turn off the ventilator, and the shell that was Jahi will stop using oxygen. Jahi's not in this fight, a bunch of cells are on autopilot doing what they'd be doing anyway, replicating and spinal nerve reflex twitching every so often. That poor child, what a horrible thing to be remembered for!
This sounds a lot like Carol J Burt. She believes the apnea tests are deadly and brain death is all about getting our organs whether we want to give them or not. Her tinfoil has been way too tight for way too long.
Deleteapparently she has not read the part where it says to immediately terminate the test if the O2 saturation drops below 80%
DeleteI found that on a webpage showing the tests performed. I noticed it did not say "if the EEG shows absolutely no electrical energy present" or "unless the MRI shows any of the brain has not degraded into mush"
Doc - I'm trying to wrap my head around the fact that a body has been maintained this long, if indeed, this is true. Do YOU believe Jahi's body is still being "maintained", for lack of a better word? Or do you think it is a hoax? I would think it would be a tremendous effort of coordination and skill to keep a brain dead body "around" for any length of time - and despite the gruesome predictions of what would transpire, we are led to believe this is going on in a private apartment? Isn't this some kind of a record, and can anything be learned from this, medically? Apart from the aspect of being a cautionary tale? Love your blog, would appreciate any thoughts.
ReplyDeletethey can grow hamburger in a petri dish. as long as you can maintain oxygen and nutrition to a cell, the cell will persist for as long as its genetic code remains intact and it does not suffer damage.
DeleteI have little doubt that her body is still on machines and being maintained with enteric tube feeds and a ventilator. She is not the first to be maintained in such a manner - there is a case study from Japan (I believe) where a brain dead patient was kept on machines for about 20 years.
DeleteIt is a large effort to keep someone in such a state, and I'm impressed they've kept it up for this long.
There is always something to learn medically, especially in cases like this which are fleetingly rare. There are no reports of brain dead patients starting menses. Now there is one. Supposedly.
Doc, they are claiming that she has an intact hypothalamic- pituitary- ovarian axis and that is why she has started menses. It appears from the MRI that they showed that area of the brain has been destroyed. They've shown no actual proof or described it in any way, such as whether it occurs in normal cyclical manner. Who exactly said it was menstruation to begin with? Perhaps these doctors are simply repeating what they've been told since none of them have actually examined her.
Deleteis it menses or is it just her uterus breaking down?
DeleteIt could be anything. She has diabetes and that can cause irregular bleeding, as could the hormone treatments used to stop infections. We don't know her medical history really, she could have something like endometriosis, or cysts, fibroid, etc...
DeleteThe only thing that's certain is that she's bleeding. But seeing as how she's 13, I'd put money on her cycle stopping up until now and suddenly bleeding recently. Which means it's probably not actually menses, an infection or other medical problem.
Typo.
DeleteWhich means it's probably not actually menses, -but- an infection or other medical problem.
the house of cards seems to be falling apart rather rapidly.
DeleteShe does not have diabetes.
DeleteThis comment has been removed by a blog administrator.
ReplyDeleteAh, I was wondering if you were banned or not yet.
DeleteJohnny,hit and run again,try to be a man and face the music
DeleteAnother trolling comment deleted.
DeleteGoldenShellback isn't the first (nor the smartest) to cry "Fake!", and he will not be the last. That's the price I pay for remaining anonymous.
ALL trolling comments will be deleted with alacrity.
I wish I had a delete troll button....
Deletethere's only one person I suspect of being a faker around here, and it ain't the good doctor...
DeleteThink about those frogs or pigs students dissect in high school. You could pump blood into any one of them, you could get reflexes out of them with a little electricity; hell, you could even restart their heart if you managed to get to them soon enough. It still doesn't mean they're alive. My heart does go out to the family for having their grief drawn out like this. Death is never easy to deal with, and a child's death is possibly the hardest to bear. Because of that, I can understand their denial even though I don't agree with it.
ReplyDeleteI think Dolan would have had a much better argument re Jahi's responding to her mother's commands had they posted the video of Jahi getting into the Lotus position all by herself.
ReplyDeleteI don't know GoldenShellback but I'm having a difficult time understanding why he presents ideas and then starts name calling rather than continue with an intellectual discussion. I guess that's the defining characteristic of a troll?
Because they are nothing but sheeples. The ones who were brought up in the South. The right wingers with their fascist ideology.
DeleteGoldenShellback is all over the internet by another name,this is what he does,he posts some untrue things to discredit people,none of it is true but that hasn't stopped him,he thinks if even one person believes him he has won
DeleteGoldenShellback said "sheeples" and "fascist". I'm going to leave that comment up just so everyone can bask in the sheer, unadulterated stupidity of it.
DeleteEnjoy, everyone.
we know who made these comments ,nothing will change my mind about who you are and what you do
DeleteYes, that actually is the best Johnny can do. What's pathetic is that he's looking for his own sheeples and those sheeples would be ok. Anyone who believes something different is a bad sheeple. That's some serious fail logic but that's Johnny in a nutshell. FAIL.
Delete^^^^^^ i wish i could up vote you for this
Deletehe is a topic stalker, and not much else. he knows how to cut and paste but as soon as you throw original data into the mix, he falls all apart; because he can't figure out how to deal with it. and apparently he has something against corn.
DeleteThis comment has been removed by a blog administrator.
DeleteSo you get owned by docbastard and move to attacking other commenters? That's pretty sad. Why not regale docbastard(and the rest of us) with your vast store of Googled medical info. Are you incapable of proving your argument?
DeleteGoldenShellback - Nope, not playing that game.
Delete